图算法

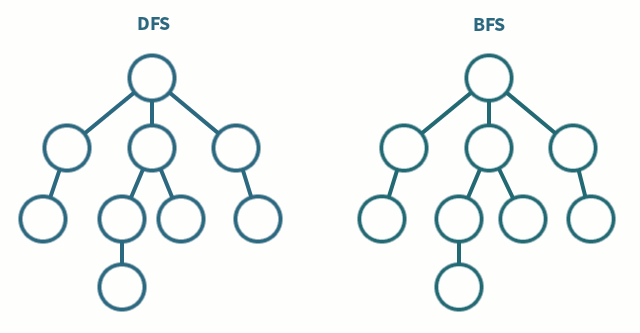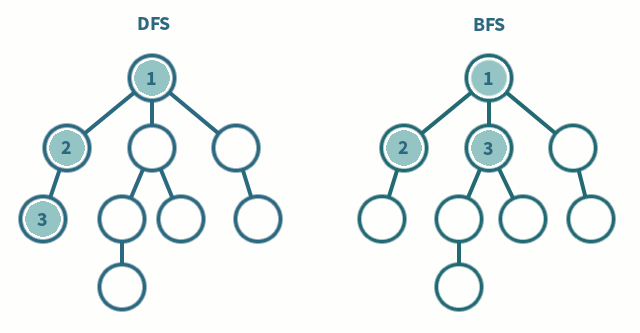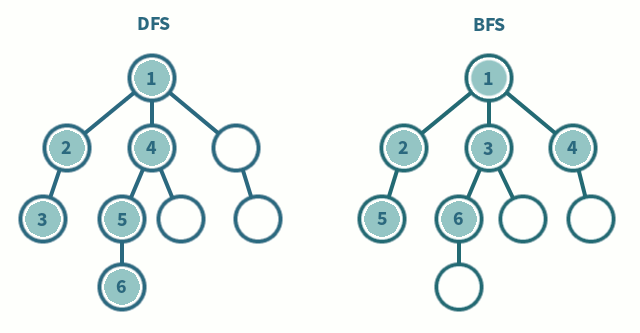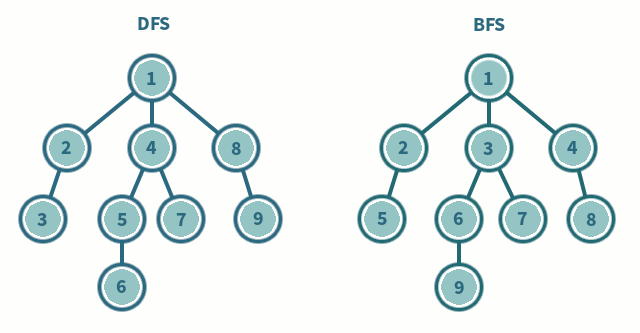
深度优先搜索

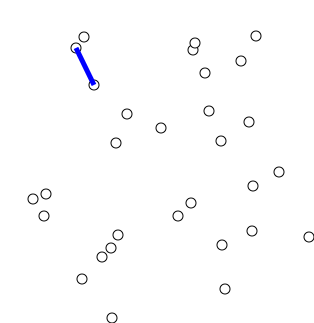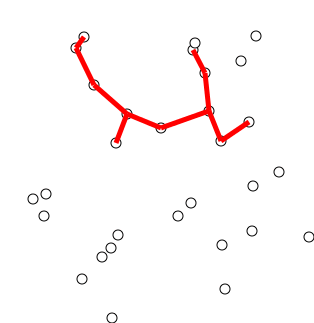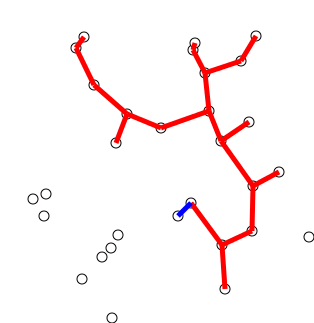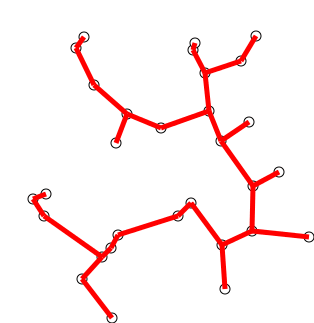
• 深度优先算法是一种优先遍历子节点而不是回溯的算法。
• 时间复杂度: O(|V| + |E|)

广度优先搜索

• 广度优先搜索是优先遍历邻居节点而不是子节点的图遍历算法。
• 时间复杂度: O(|V| + |E|)

拓扑排序

• 拓扑排序是对于有向图节点的线性排序，如果存在某条从 u 到 v 的边，则认为 u 的下标先于 v。
• 时间复杂度: O(|V| + |E|)

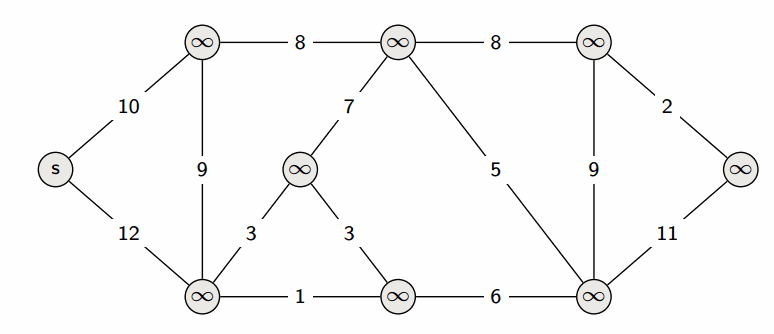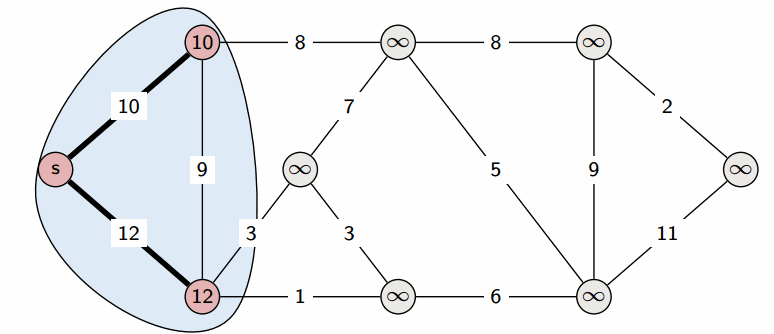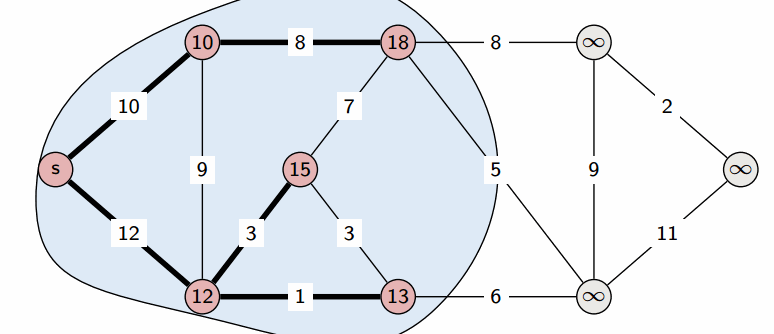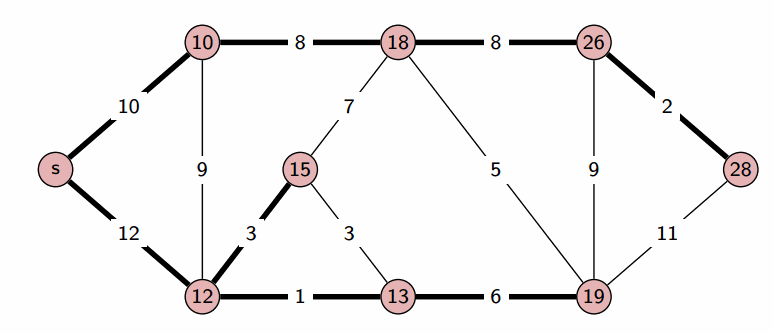
Dijkstra算法

• Dijkstra 算法 用于计算有向图中单源最短路径问题。
• 时间复杂度: O(|V|^2)

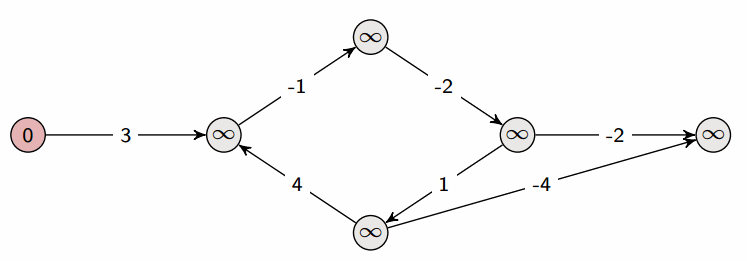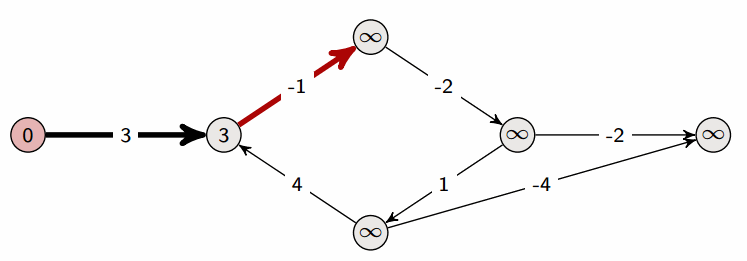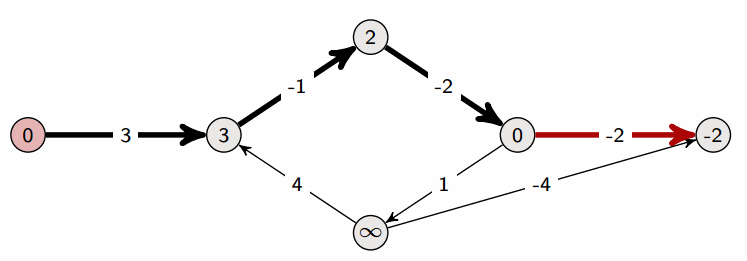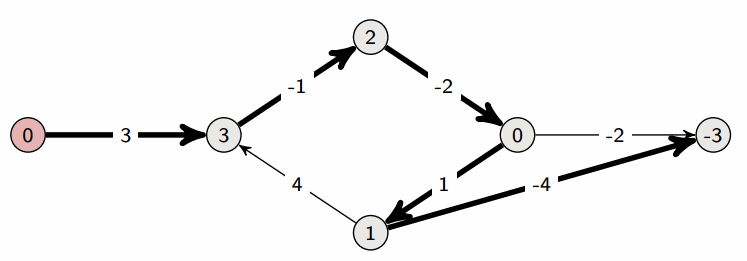
Bellman-Ford算法

• Bellman-Ford 算法是在带权图中计算从单一源点出发到其他节点的最短路径的算法。
• 尽管算法复杂度大于 Dijkstra 算法，但是它适用于包含了负值边的图。
• 时间复杂度:
  • 最优时间: O(|E|)
  • 最坏时间: O(|V||E|)

Floyd-Warshall算法

• Floyd-Warshall 算法 能够用于在无环带权图中寻找任意节点的最短路径。
• 时间复杂度:
  • 最优时间: O(|V|^3)
  • 最坏时间: O(|V|^3)
  • 平均时间: O(|V|^3)

Prim算法

• Prim 算法是用于在带权无向图中计算最小生成树的贪婪算法。换言之，Prim 算法能够在图中抽取出连接所有节点的边的最小代价子集。
• 时间复杂度: O(|V|^2)

Kruskal算法

• Kruskal 算法同样是计算图的最小生成树的算法，与 Prim 的区别在于并不需要图是连通的。
• 时间复杂度: O(|E|log|V|)